Who doesn’t like chess? Me! Sure, I like the idea of chess – intellectual masterminds battling each other using nothing but pure thought – the problem is that I tend to lose, probably because I don’t really know how to play well, and because I never practice. I do know one thing: How much the different pieces are worth, their point values:

This was among the first things I learned when I was taught chess by my father. Given these point values it should be as valuable to have a knight on the board as having three pawns, for example. So where do these values come from? The point values are not actually part of the rules for chess, but are rather just used as a guideline when trading pieces, and they seem to be based on the expert judgment of chess authorities. (According to the guardian of truth there are many alternative valuations, all in the same ballpark as above.) As I recently learned that it is very important to be able to write Big Data on your CV, I decided to see if these point values could be retrieved using zero expert judgement in favor of huge amounts of chess game data.
The method
How to allocate point values to the chess pieces using only data? One way of doing this is to calculate the predictive values of the chess pieces. That is, given that we only know the current number of pieces in a game of chess and use that information to predict the outcome of that game, how much does each type of piece contribute to the prediction? We need a model to predict the outcome of chess games where we have the following restrictions:
- Each type of piece has a single point value that directly contributes to the predicted outcome of the game, so no interaction effects between the pieces.
- The value of a piece does not change over the course of the game.
- Use no context and nor positional information.
Now these restrictions might feel a bit restrictive, especially if we actually would want to predict the outcome of chess games as well as possible, but they come from that the original point values follow the same restrictions. As the original point values doesn’t change with context, neither should ours. Now, as my colleague Can Kabadayi (with an ELO well above 2000) remarked: “But context is everything in Chess!”. Absolutely, but I’m not trying to do anything profound here, this is just a fun exercise! :)
Given the restrictions there is one obvious model: Logistic regression, a vanilla statistical model that calculates the probability of a binary event, like a loss-win. To get it going I needed data and the biggest Big Data data set I could find was the Million Base 2.2 which contains over 2.2 million chess games. I had to do a fair deal of data munging to get it into a format that I could work with, but the final result was a table with a lot of rows that looked like this:
pawn_diff rook_diff knight_diff bishop_diff queen_diff white_win
1 0 1 -1 0 TRUE
Here each row is from a position in a game where a positive number means White has more of that piece. For the position above white has one more pawn and knight, but one less bishop than Black. Last in each row we get to know whether White won or lost in the end, as logistic regression assumes a binary outcome I discarded all games that ended in a draw. My résumé is unfortunately not going to look that good as I never really solved the Big Data problem well. Two million chess games are a lot of games and it took my poor old laptop over a day to process only the first 100,000 games. Then I had the classic Big Data problem that I couldn’t fit it all into working memory, so I simply threw away data until worked. Still, for the analysis I ended up using a sample of 1,000,000 chess positions from the first 100,000 games in the Million Base 2.2 . Big enough data for me.
The result
Using the statistical language R I first fitted the following logistic model using maximum likelihood (here described by R’s formula language):
white_win ~ 1 + pawn_diff + knight_diff + bishop_diff + rook_diff + queen_diff
This resulted in the following piece values:
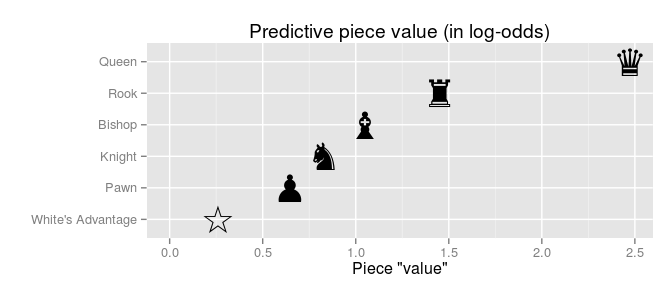
Three things to note: (1) In addition to the piece values, the model also included a coefficient for the advantage of going first, called White’s advantage above. (2) The predictive piece values ranks the pieces in the same order as the original piece values does. (3) The piece values are given in log-odds, which can be a bit tricky to interpret but that can be easily transformed into probabilities as this graph shows:
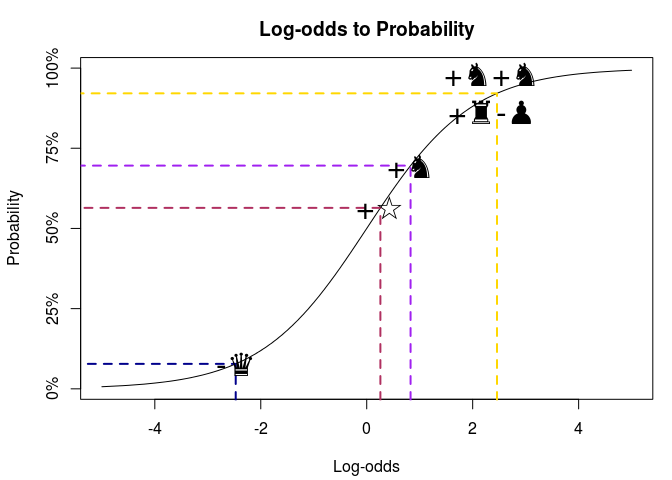
Here White’s advantage translates to a 56% chance of White winning (everything else being equal), being two knights and one rook ahead but one pawn behind gives 92% chance of winning, while being one queen behind gives only a 8% chance of winning. While log-odds are useful if you want to calculate probabilities, the original piece values are not given in log-odds, instead they are set relative to the value of a pawn which is fixed at 1.0 . Let’s scale our log-odds so that the pawn is give a piece value of 1.0 :
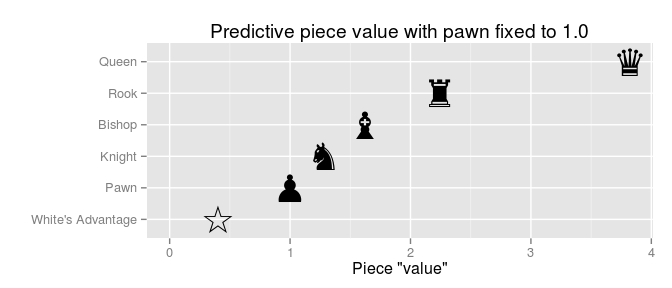
We see now that, while the ranking is roughly the same, the scale is compressed compared to the original piece values. A queen is usually considered as nine times more valuable than a pawn, yet when it comes to predicting the outcome of a game a queen advantage counts the same as only a four pawn advantage. A second thing to notice is that bishops are valued slightly higher than knights. If you look at the Wiki page for Chess piece relative value you find that some alternative valuations value the bishop slightly higher than the knight, others add ½ point for a complete bishop pair. We can add that to the model!
white_win ~ 1 + pawn_diff + knight_diff + bishop_diff + rook_diff + queen_diff + bishop_pair_diff
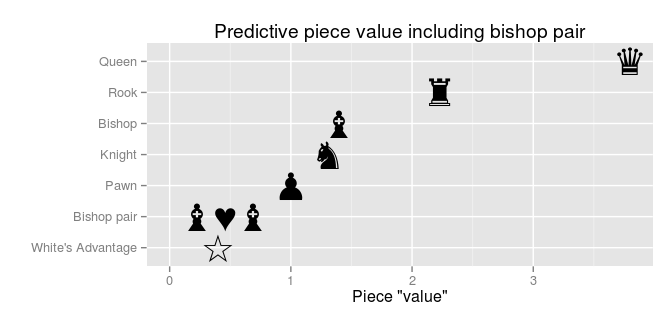
Now with a pair of bishops getting their own value, the values of a knight and a single bishop are roughly equal. There is still the “mystery” regarding the low valuation of all the pieces compared to the pawn. (This doesn’t really have to be a mystery as there is no reason why predictive piece values necessarily should be the same as the original piece values). Instead of anchoring the value of a pawn to 1.0 we could anchor the value of another piece to it’s original piece value. Let’s anchor the knight to 3.0:
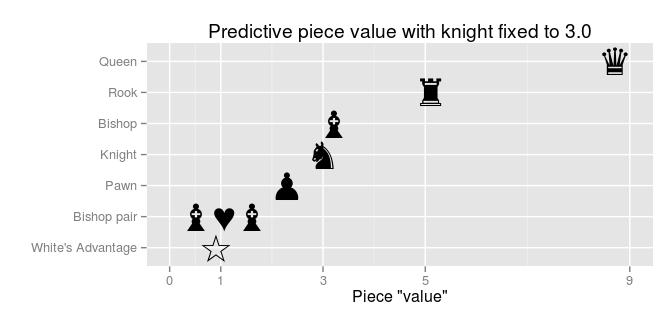
Now the value of the pieces (excluding the pawn) line up very nicely with the original piece values! So, as I don’t really play chess, I don’t know why a pawn advantage is such a strong predictor of winning (compared to the original piece values, that is). My colleague Can Kabadayi (the ELO > 2000 guy!) had the following to say:
In a high-class game the pawns can be more valuable – they are often the decisive element of the outcome – one can even say that the whole plan of the middle game is to munch a pawn somewhere and then convert it in the endgame by exchanging the pieces, thus increasing the value of the pawn. Grandmaster games tend to go to a rook endgame where both sides have a rook but one side has an extra pawn. It is not easy to convert these positions into a win, but you see the general idea. A passed pawn (a pawn that does not have any enemy pawns blocking its march to become a queen) is also an important asset in chess, as they are a constant threat to become a queen.
Can also gave me two quotes from legendary chess Grandmasters José Capablanca and Paul Keres relating to the value of pawns:
The winning of a pawn among good players of even strength often means the winning of the game. – Jose Capablanca
The older I grow, the more I value pawns. – Paul Keres
Another thing to keep in mind is that the predictive piece values might have looked very difference if I had used a different data set. For example, the players in the current data set are all very skilled, having a median ELO of 2400 and with 95% of the players having an ELO between 2145 and 2660. Still I think it is cool that the predictive piece values matched the original piece values as well as they did!
Update: See the follow-up where I look at how the predictive point values change as the game progresses.
Final notes
- Again, I don’t know much about chess, but the the Million Base 2.2 is a fun database to work with, so if you have any suggestion for other things to look at, leave a comment below or tweet me ( @rabaath)!
- If you want to dabble with the database yourself you can find the scripts I used to convert the data in the Million Base into an analysis friendly format, and the code for recreating the predictive piece value analysis, here:
- Python script to convert the Million Base 2.2 to a json-format:
- R scripts that recreates the analysis and plots in this post:
- While “researching” this post I learned about this really fun chess variant called Knightmare Chess which plays like normal chess but with the addition that each player can play action cards with “special effects”. These effects are often spectacular, like the card Fireball that “explodes” a piece which kills all adjacent pieces. This add a (large) element of randomness to the game, which might irritate chess purist, but makes it possible for me to win once in a while :)