The t-test is probably the most used and abused statistical test in research [ Citation Needed]. The t-test is used when you have two groups of measures and you want to look at the difference between the groups and the original t-test assumes that the measures are approximately normally distributed and that the two groups have equal variance. While this last assumption is relaxed by Welch’s t-test a large problem remains: The t-test isn’t Bayesian :)

John Kruschke has deviced a Bayesian model that can be used as a drop in replacement for the classical t-test and that he boastingly dubbed BEST (Bayesian EStimation Supersedes the T-test). Instead of uninformative p-values it gives you the actual probability that the two groups are different (given the model), isn’t that nice? BEST even adds some more bells and whistles, the data (not the sampling distribution as in the original t-test) is assumed to come from a t-distribution with an unknown degrees of freedom and as the t-distribution has thicker tails than the normal distribution this helps reducing the influence of outliers in the data. BEST also estimates many more parameters than just the difference between the groups, for example, the difference in variance and the effect size. The full model used by BEST is given in this diagram:

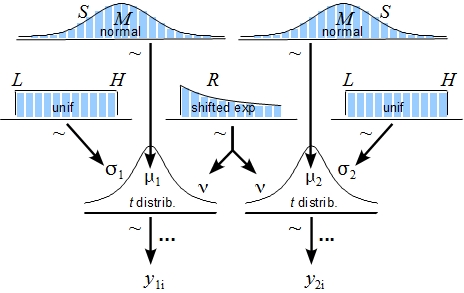
So what is my contribution to all this? Well, I’ve made an online version of BEST that lets you do Bayesian statistics in your browser! I was interested mainly in how well javascript would handle the relatively heavy Markov Chain Montecarlo simulations necessary to run many Bayesian models and BEST seemed like a good target. Turns out it works really well, javascript is pretty fast and with the help of the FLOT library it was easy to create nice looking plots of the analysis. Try it out at https://sumsar.net/best_online/!