Hello stranger, and welcome! 👋😊
I'm Rasmus Bååth, data scientist, engineering manager, father, husband, tinkerer,
tweaker, coffee brewer, tea steeper, and, occasionally, publisher of stuff I find
interesting down below👇
Sometimes it feels a bit silly when a simple statistical model has a
fancy-sounding name. But it also feels good to drop the following in
casual conversation: “Ah, then I recommend a Plackett-Luce model, a
straightforward generalization of the Bradley–Terry model, you know”,
when a friend wonders how they could model their, say, pinball
championship dataset. Incidentally, in this post we’re going to model
the result of the IFPA 18 World Pinball Championship using a
Plackett-Luce model, implemented in Stan as a generalization of the
Bradley–Terry model, you know.
I know neither who Bradley, Terry, Plackett, nor Luce were, but I know
when their models could be useful:
This is just a post to brag about that
the CopenhagenR useR group is alive and kicking, again.
After COVID-19, the group (like so many other meetups) was on hiatus for a couple of years and without an organizer. In 2023, I thought I would try starting it again and, while it took a little while, I’m happy that I got together five great meetups for the spring 2024 season! Here’s a little bit about what went down.
There are tons of well-known global indicators. We’ve all heard of gross
domestic product, life expectancy, rate of literacy, etc. But, ever
since I discovered
pinballmap.com, possibly
the world’s most comprehensive database of public pinball locations,
I’ve been thinking about a potential new global indicator: Public
Pinball Machines per Capita. Thanks to Pinball Map’s
well-documented
public API, this indicator
is now a reality!
Here’s how this was
put together (and just scroll to the bottom for a CSV file with this
indicator for all countries).
Upon discovering that the tiny town I live in has a pinball arcade with
over 40 tables (!), I got a bout of pinball fever. I fancy myself a
fairly accomplished video game player, but was disappointed to discover
that my ability to keep Mario alive didn’t translate to preventing the
pinball from draining. Assuming I just needed a bit of practice, I
downloaded
a virtual version of Fish
Tales — a fun,
fishing-based table from 1992 — and began practicing. Here’s the data
and quick analysis of how I improved over 100 games of Fish Tales.
(By the way, if you didn’t know, the hobbyist pinball emulation scene is
amazing. Almost every real pinball table from the last 70 years has
been painstakingly 3D-model by someone and is
available completely
for free, but completely not legally…)
Five years ago I started a new role and I suddenly found myself, a
staunch R fan, having to code in Python on a daily basis. Working with
data, most of my Python work involved using
pandas, the Python data frame library,
and initially I found it quite hard and clunky to use, being used to the
silky smooth API of R’s
tidyverse. And
you know what? It still feels hard and clunky, even now, 5 years later!
But, what seems even harder, is explaining to “Python people” what they
are missing out on. From their perspective, pandas is this fantastic
tool that makes Data Science in Python possible. And it is a fantastic
tool, don’t get me wrong, but if you, like me, end up in many “pandas is
great, but…”-type discussions and are lacking clear examples to link to;
here’s a somewhat typical example of a simple analysis, built from the
ground up, that flows nicely in R and the tidyverse but that becomes
clunky and complicated using Python and pandas.
Let’s first step through a short analysis of purchases using R and the
tidyverse. After that we’ll see how the same solution using Python and
pandas compares.
Now that I’ve got my hands on
the source of the cake
dataset I knew I had to attempt to
bake the cake too. Here, the emphasis is on attempt, as there’s no way
I would be able to actually replicate
the elaborate and
cake-scientifically rigorous
recipe that Cook
followed in her thesis. Skipping things like beating the eggs exactly
“125 strokes with a rotary beater” or wrapping the grated chocolate “in
waxed paper, while white wrapping paper was used for the other
ingredients”, here’s my version of Cook’s Recipe C, the highest rated
cake recipe in the thesis:
~~ Frances E. Cook's best chocolate cake ~~
- 112 g butter (at room temperature, not straight from the fridge!)
- 225 g sugar
- ½ teaspoon vanilla, extract or sugar.
- ¼ teaspoon salt
- 96 g eggs, beaten (that would be two small eggs)
- 57 g dark chocolate (regular dark chocolate, not the 85% masochistic kind)
- 122 g milk (that is, ½ a cup)
- 150 g wheat flour
- 2½ teaspoon baking powder
1. In a bowl mix together the butter, sugar, vanilla, and salt
using a hand or stand mixer.
2. Add the eggs and continue mixing for another minute.
3. Melt the chocolate in a water bath or in a microwave oven.
Add it to the bowl and mix until it's uniformly incorporated.
4. Add the milk and mix some more.
5. In a separate bowl combine the flour and the baking powder.
Add it to the batter, while mixing, until it's all combined evenly.
6. To a "standard-sized" cake pan (around 22 cm/9 inches in diameter)
add a coating of butter and flour to avoid cake stickage.
7. Add the batter to the pan and bake in the middle of the oven
at 225°C (437°F) for 24 minutes.
Here’s now some notes, photos, and data on how the actual cake bake went
down.
In statistics, there are a number of classic datasets that pop up in examples, tutorials, etc. There’s
the infamous iris dataset (just type iris in your nearest R prompt),
the Palmer penguins (the modern iris replacement),
the titanic dataset(s) (I hope you’re not a guy in 3rd class!), etc. While looking for a dataset to illustrate a simple hierarchical model I stumbled upon another one: The cake dataset in
the lme4 package which is described as containing “data on the breakage angle of chocolate cakes made with three different recipes and baked at six different temperatures [as] presented in Cook (1938)”. For me, this raised a lot of questions: Why measure the breakage angle of chocolate cakes? Why was this data collected? And what were the recipes?
I assumed the answers to my questions would be found in Cook (1938) but, after a fair bit of flustered searching, I realized that this scholarly work, despite its obvious relevance to society, was nowhere to be found online. However, I managed to track down that there existed a hard copy at Iowa State University, accessible only to faculty staff.
The tl;dr: After receiving help from several kind people at Iowa State University, I received a scanned version of Frances E. Cook’s Master’s thesis, the source of the cake dataset. Here it is:
Cook, Frances E. (1938). Chocolate cake: I. Optimum baking temperature. (Master’s thesis, Iowa State College).
It contains it all, the background, the details, and the cake recipes! Here’s some more details on the cake dataset, how I got help finding its source, and, finally, the cake recipes.
If you know one thing about bubble sort, it’s that it’s a horrible sorting algorithm. But Bubble sort is great for one thing. Bubble sort has one good use case: Beer tasting. Let me explain:
I’ve now been in the industry long enough to know that meetings are often too long. No one likes to be in meetings, and the longer they are, the worse it is. Not only do I know most meetings are too long, but I also know exactly how long a meeting should be, at most! Let’s not delay it any further; here’s Rasmus’s maximum meeting length formula:
You can see that I’m confident about the correctness of this formula, as I’ve already branded it with my own name and rendered it in $\LaTeX$.
If that’s not enough to convince you, let me break it down further:
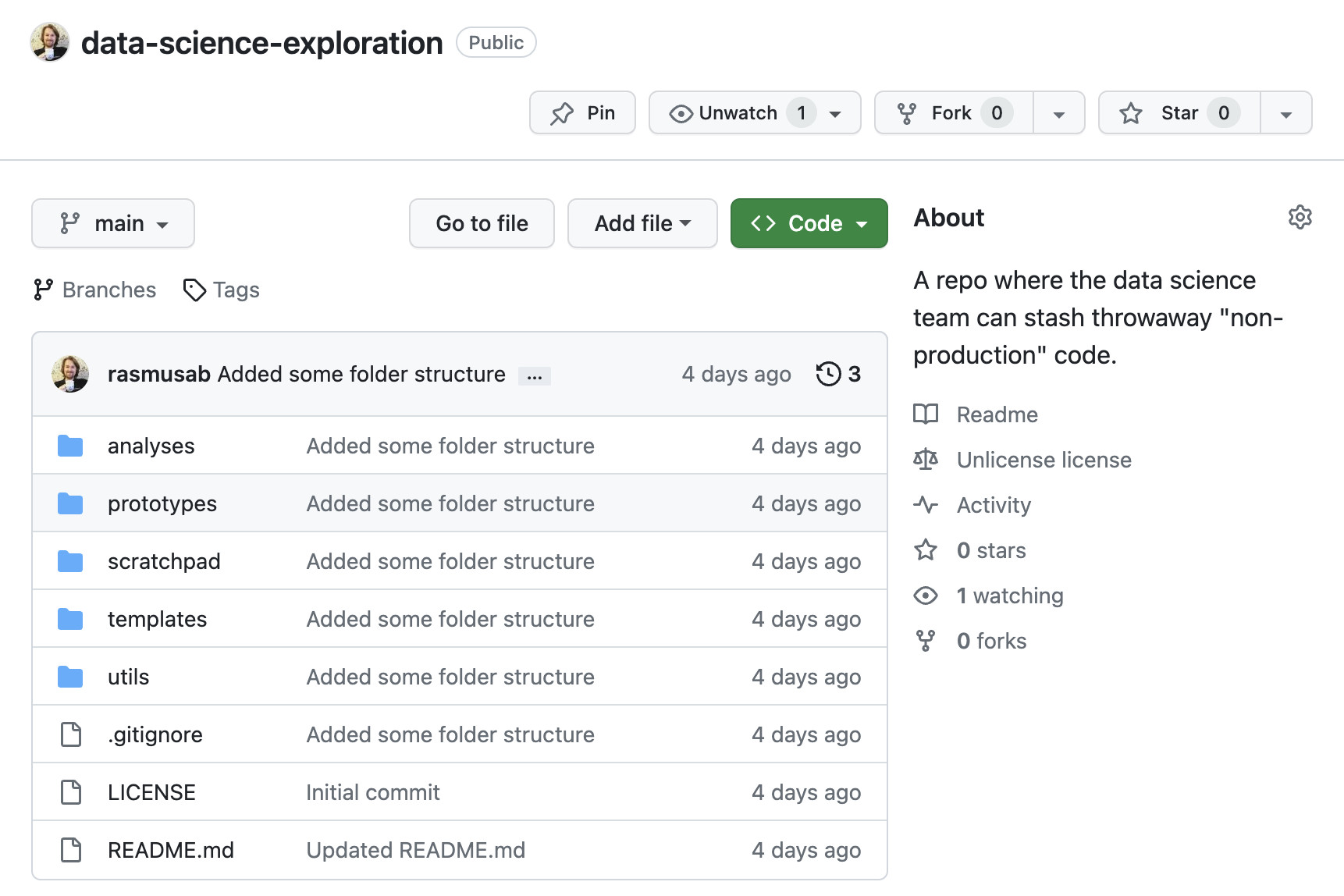
When I started working as a Data Scientist nearly ten years ago, the data science team I joined did something I found really strange at first: They had a single GitHub repo where they put all their “throwaway” code. An R script to produce some plots for a presentation, a Python notebook with a machine learning proof-of-concept, a bash script for cleaning some logs. It all went into the same repo. Initially, this felt sloppy to me, and sure, there are better ways to organize code, but I’ve come to learn that not having a single place for throwaway code in a team is far worse. Without a place for throwaway code, what’s going to happen is:
- Some ambitious person on the team will create a new GitHub repo for every single analysis/POC/thing they do, “swamping” the GitHub namespace.
- Some others will stow their code on the company wiki or drop it in the team Slack channel.
- But most people aren’t going to put it anywhere, and we all know that code “available on request” often isn’t available at all.
So, in all teams I’ve worked in, I’ve set up a GitHub repo that looks something like this:
